Graph Coloring over Adjacency List

Source: R/RcppExports.R, R/color.R

These functions perform graph coloring using various algorithms over an adjacency list.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color; this is called a vertex coloring.

graph_coloring_dsatur(adj_list)

graph_coloring_msc(adj_list)

graph_coloring_lmxrlf(adj_list)

graph_coloring_hybrid_dsatur_tabucol(adj_list)

graph_coloring_hybrid_lmxrlf_tabucol(adj_list)

graph_coloring_tabucol(adj_list, k)

Arguments

adj_list

an adjacency list in the format of list of integer vector. The outer list should enumerate nodes comprehensively and each integer vector enumerates corresponding neighboring nodes
k

number of colors to use for graph coloring

Details

graph_coloring_hybrid_dsatur_tabucol() and graph_coloring_hybrid_lmxrlf_tabucol() use a hybrid approach to run DSATUR and lmXRLF first to determine an upper bound for the graph chromatic number. It then searches better solutions by running lowered chromatic number through TabuCol to check if the graph can be colored with less colors.

Functions

  • graph_coloring_dsatur: Color graph using DSATUR algorithm (Brélaz 1979)

  • graph_coloring_msc: Color graph using Maximum Cardinality Search(MCS) algorithm (Palsberg 2007)

  • graph_coloring_lmxrlf: Color graph using Least-constraining Most-constrained eXtended RLF(lmXRLF) algorithm (Kirovski et al. 1998)

  • graph_coloring_hybrid_dsatur_tabucol: Color graph using a hybrid of DASTUR and TabuCol algorithm (Kirovski et al. 1998; Brélaz 1979; Hertz and de Werra 1987)

  • graph_coloring_hybrid_lmxrlf_tabucol: Color graph using a hybrid of lmXRLF and TabuCol algorithm (Kirovski et al. 1998; Hertz and de Werra 1987)

  • graph_coloring_tabucol: Color graph using TabuCol algorithm (Hertz and de Werra 1987)

References

https://en.wikipedia.org/wiki/Graph_coloring

https://github.com/brrcrites/GraphColoring

Brélaz D (1979). “New Methods to Color the Vertices of a Graph.” Commun. ACM, 22(4), 251--256. ISSN 0001-0782, doi: 10.1145/359094.359101 , http://doi.acm.org/10.1145/359094.359101.

Palsberg J (2007). “Register Allocation via Coloring of Chordal Graphs.” In Proceedings of the Thirteenth Australasian Symposium on Theory of Computing - Volume 65, series CATS '07, 3--3. ISBN 1-920-68246-5, http://dl.acm.org/citation.cfm?id=1273694.1273695.

Kirovski D, Potkonjak M, Potkonjak M (1998). “Efficient Coloring of a Large Spectrum of Graphs.” In Proceedings of the 35th Annual Design Automation Conference, series DAC '98, 427--432. ISBN 0-89791-964-5, doi: 10.1145/277044.277165 , http://doi.acm.org/10.1145/277044.277165.

Hertz A, de Werra D (1987). “Using Tabu Search Techniques for Graph Coloring.” Computing, 39(4), 345--351. ISSN 0010-485X, doi: 10.1007/BF02239976 , http://dx.doi.org/10.1007/BF02239976.

See also

color_graph()

Examples

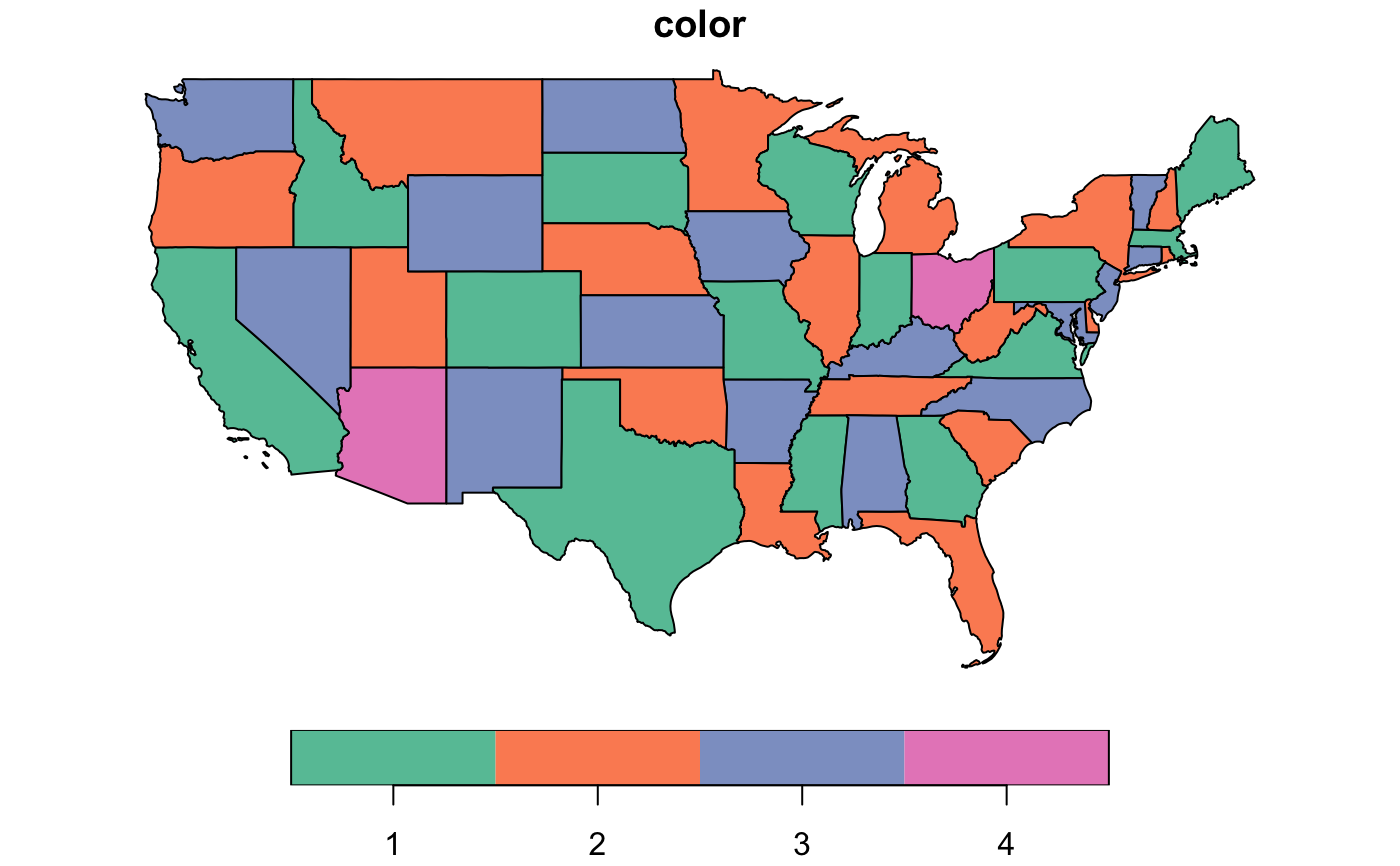
library(tidygraph)

if (requireNamespace("sf", quietly = TRUE) && requireNamespace("USAboundaries", quietly = TRUE)) {
 library(sf)
 library(USAboundaries)

 us_states() %>%
   filter(!(name %in% c("Alaska", "District of Columbia", "Hawaii", "Puerto Rico"))) %>%
   transmute(
     color = st_intersects(.) %>%
       graph_coloring_dsatur() %>%
       as.factor()
     ) %>%
   plot()
}
#> Linking to GEOS 3.6.1, GDAL 2.1.3, proj.4 4.9.3
#> although coordinates are longitude/latitude, st_intersects assumes that they are planar
#> although coordinates are longitude/latitude, st_intersects assumes that they are planar